《微积分的力量》读书报告
主题:微积分是上帝的语言,无所不在,充满力量
发展历经三个方面:几何、运动、变化
核心问题:3个问题->2个问题
应用:在现代前沿科学技术领域中的应用
emm我的总结梳理能力比较欠缺,这是我第一次尝试梳理一本书的内容来分享~ 有些地方本来有书中配图会更好,但我书没带。
首先说说读这本书的感受吧
我们平常网上找资料、看书,目的都是干货。 能够解决眼前问题 燃眉之急
但干货就像干巴巴的面包,要真正消化吸收不容易。 通常都是为了果腹 迫不得已而为之
而这本书就像是一个水果,可以促进消化系统。 长期受益
这本书写的很精致。为什么这么说呢?倒不是指外观,而是指内容安排。书中用了很多例子,打了很多比喻。例子多是说明微积分的起源、发展、应用。从阿基米德、伽利略、笛卡尔、费马、牛顿、莱布尼兹、到拉普拉斯、爱因斯坦等。例子多并不足夸道,但是这些例子作者用的恰到好处,连接的行云流水,话语通俗而又不失准确性。
十分推荐阅读,读完对微积分和数学产生了亲切感,好像提升了对数学的敏感度,打个不恰当的比方,在大学时关于这方面的学习,使我全身紧绷又僵硬,学完这本书则像是在温泉里泡了半小时,全身毛孔舒张。
至于收获多少可能又会因人而异。像我机缘有限就收获了这些。但也足够了。
微积分
几何
微积分是几何学的产物
圆是一种很特别的形状,它十分完美。大自然中圆无处不在,当我们凝视圆的时候,圆实际上也在注视着我们,因为它们就在我们所爱之人的瞳孔和虹膜的圆形轮廓中。 源于生活。
内容上,从无穷说起,关于无穷的思考来自于几何问题。
曲边形面积(曲面积)
无穷来源于曲线,因为矩形的面积一目了然,而人们对圆的面积一无所知,阿基米德等痴迷几何的科学家想到用已知来逼近未知的方法。内接一个正方形、再把每一条边分成相等的两条边得到正八边形……如此一直分下去……人们仿佛看到了无穷,无穷的尽头似乎是一个光滑的圆。主观上说来是的,但客观上来说却不是!无论分的多微小,只要显微镜的放大倍数足够大,光滑圆就会崩解成一段段直线~
微积分的几何表达:
让多边形变得光滑连续,就是积分的工作;
让光滑连续的圆崩解成一条条线段,这就是微分。
微积分可分为两个步骤:切分和重组。如上所述,用数学术语来说,切分过程总是涉及无限精密的减法运算,用于量化各部分之间的差异,这个部分叫做微分学。重组过程则总是涉及无限的加法运算,将各个部分整合成原来的整体,这个部分叫做积分学。
曲线求面积问题是积分学的圣杯,因为很多其它问题都可归结为这个问题。
从现代的角度,面积问题旨在预测以不断变化的速率变化(变加速度运动)的事物与它随时间的累积程度之间的关系
牛顿提出流数术
-
流量(现在认为是指时间的函数),流数是指流量的导数,或随时间的变化率
-
明确了微积分的两个核心问题:
- 已知流量求流数 求导 即微分!
- 局部问题 舍弃了显微镜所关注的那点的无穷小邻域以外的所有细节
- 已知流数求它们的流量 面积问题的关键所在 根据变化率推导未知函数 根据斜率推导曲线 积分
- 整体问题 是用望远镜遥望远方,预测未来,所有干预事件都很重要不能被忽略。
- 已知流量求流数 求导 即微分!
整体问题比局部问题难得多!
运动
解析几何是一个强大的工具
已知物体位置随时间的变化,如何求物体速度随时间的变化
- 微分:放大——局部——变化率!
可见运动中就体现了变化
通过解析几何将这一运动问题转化成几何问题——斜率
关于已知物体运动速度随时间的变化规律,如何求物体位置随时间的变化
- 积分:由变化率求曲线=反向问题
解决方法是求曲线与时间轴所围的面积随时间的累积
通过解析几何将这一运动问题转变成了几何问题——曲面积
微积分的核心——无穷
无穷原则从一开始就存在!微积分可以用它的信条来定义:在解决关于任意连续体的难题时,先把它切分成无穷多个部分,然后一一求解,最后通过把各个部分的答案组合起来去解决原始的难题。这也是无穷原则的定义。
微积分的三大核心问题
- 正向问题 已知一条曲线,求他各处的斜率 求导
- 反向问题 已知一条曲线各处的斜率,求这条曲线 积分
- 面积问题 已知一条曲线求它下方的面积 积分
看书之前对微积分的认知也就停留在这了。但这本书却讲了300多页这么厚,那么要么是废话,要么就是精致了。而显然给我的印象是后者,作者的笔墨用的恰到好处,加深对微积分的印象、扩展对数学科学研究、科学发现方面的视野,有助于形成一个比较立体、完整的感知,知道科学研究的一些来龙去脉。
曲线下方的面积(求导)——>曲线(求导)——>曲线的斜率
反向问题和面积问题是一出生就被拆散的双胞胎,或者说是人们看到的同一枚硬币的两面,本质相同。
面积问题解决==反向问题解决。
无穷小量
- 无穷小的数
- 无穷小的长度 尽管不是一个点,但却比你能想到的任何长度都小
- 无穷小的时间 尽管不是一瞬间,但却比你能想到的任何持续时间都短。
微积分背后的核心观点
- 在很多自变量x和因变量y之间的关系问题中,输入一个小的变化量△x(偏移)都会使输出产生一个小的变化量△y
- 这个小变化量通常是以我们可利用的结构化方式组织起来的,比如y=x^3,x=(x+△x),则y=x^3 + 3·x^2·**△x **+ 3·x·△x^2 + △x^3
- 输出的变化量包含不同层级的部分,按照大小无穷小的部分还可 分级为小、超小、超超小…… 高阶无穷小量
- 我们关注占主导地位的变化量,忽略更微小的变化量
- 如果输入的变化量是有限的,比如2+0.0001,那么无疑得到的只是近似结果。
- 但如果输入的变化量△x是无穷小的,那么这种近似处理反而得到精确的结果!
- 那么处理y的三次方这个函数时,如果dx是一个无穷小的差分,dy就可以取x^3 + 3·x^2·**dx **,保留dx一次方项,是为了研究无穷小变化量!
我大学课程所学大多是通过极限的思维来讲解,但其实通过无穷小来理解更接近微积分的本质,这时它们(dx、dy)叫做微分!

无穷小量dx尽管不等于0,但也必须满足类似x+dx=x这样无意义的方程
喜悦
为什么我感受到他们的喜悦呢
大概是因为我觉得他们发现的知识是理性知识,大概从他们身上我看到了纯粹科学的非实用性、非功利性
理性的知识自己决定自己,自己推出自己 仅为自己而存在,他们是自由的知识 只有自由的知识才是确定性知识 是绝对的,很可能成为永恒正确的。
他们的科学很简单,就是出于兴趣,即使当初没有这项科学发现,对他们的生活不会产生多大影响,顶多是在酒宴上的少了一两件引以为豪的谈资。至少作者的描述让我这么觉得,于是我感受到他们的快乐。
阿基米德
出于兴趣,发现了杠杆原理 浮力原理
阿基米德 用三角形逼近抛物线弓形求其面积 无穷级数 重量想象
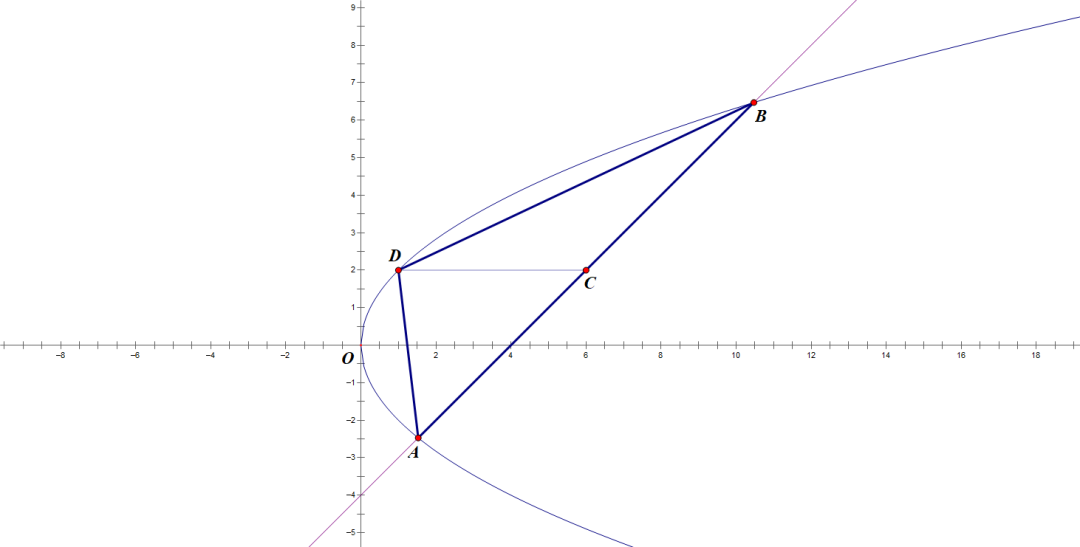
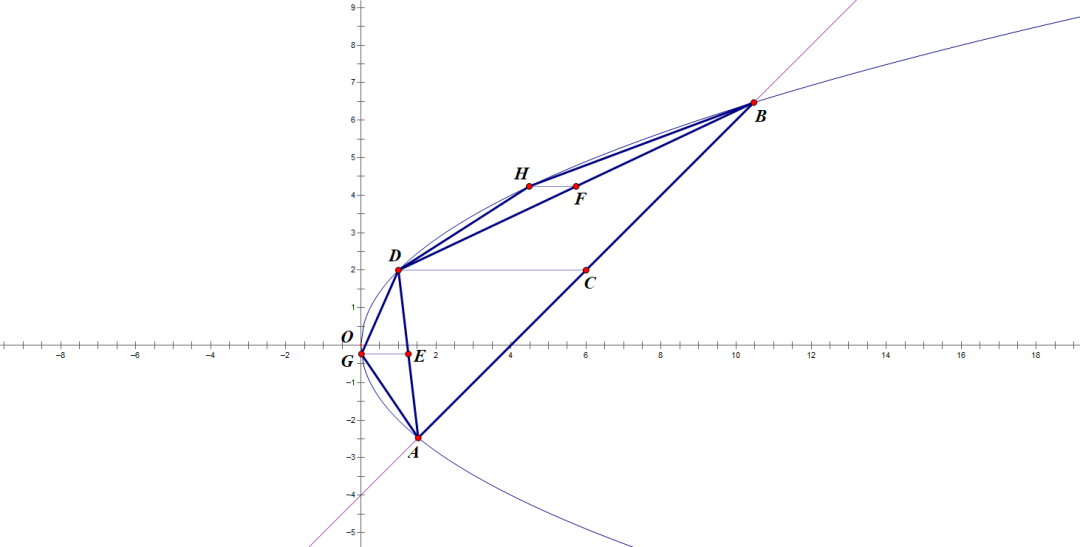
用三角形去逼近抛物线弓形的面积,第2次开始每次以三角形的边为底再做三角形,去逼近弓形。不是随便做,每次做的三角形要确保面积最大。这样做可以在增加相同逼近次数的情况下确保最拟合精度最高。
伽利略
地球上的运动——阿基米德的“学生”伽利略 捡起来阿基米德的研究 理性主义者
出于兴趣,当然还有一贯严谨作风的功劳,他发现了奇数1、3、5、7……与物体下落运动的秘密
垂直落体运动太快没有足够的科技手段进行观察记录,怎么办?于是
斜面试验——科学极简主义的艺术
“凹槽雕刻得非常平直,打磨得十分光滑”,“沿凹槽滚动的是一个坚硬光滑的铜球,非常圆”
之所以关注斜面凹槽的平直度、光滑度、球的坚硬度、圆度、光滑度,因为伽利略想让球在它能设法实现的最简单最理想的条件下滚落,尽可能减少潜在问题的影响。
伽利略对待实验十分严谨,就好像有些人痴迷于游戏、痴迷于动漫,若是能将这种热情调整到合适的方向上或许也潜力无限吧。
牛顿
牛顿是少数的出身不好的,他从一个孤寂的男孩,一步步成为科学巨人。竟也是出于兴趣爱好。从他的笔记中也能看出其喜悦吧~
幂级数法,牛顿在思考圆的面积时偶然所得。微积分运算变得毫不费力!
牛顿站在巨人的肩膀上
- 他统一、综合和归纳了伟大前辈的思想 创造了一种新事物——通用的级数法(通过变量x,他定义了无穷个无穷级数 )
- 他继承了阿基米德的无穷原则
- 他的切线知识来自费马
- 他使用的小数和变量x分别来自印度数学家和阿拉伯代数
- 他用方程表示xy平面上曲线的做法来自笛卡尔的著作
- 他对无穷的随心所欲的玩法、他的实验精神及他对猜想和归纳的开放性态度都来自沃利斯。


大凡尔赛——莱布尼兹!
莱布尼兹用微积分轻松推导出光折射的正弦定律,并且自豪的指出:“其他学识渊博的人大费周章得出的结论,精通微积分的人却好像拥有魔法一样,只做了几步推导就搞定了。”
莱布尼兹转行到数学,从谦卑求学,到与巨人比肩,其中的喜悦也是溢于言表~
启发
书中很多东西,让我眼前一亮,有些是新奇,有些是触动了即将被遗忘的记忆。蛮有趣的~
模式!
这个词似乎很重要!很多科学发现,就是在用某个模式去拟合真实物理现象
类似于开普勒和伽利略他们发现的那些模式。 第三定律(相同时间扫过面积相同) 下落物体相同时间位移变化满足比例1:3:5:7……奇数比
自然规律 用人类的语言描述出来就成了模式~
惠更斯级数求和问题,促使莱布尼兹发现了积分的奥秘 类比!:高度计测台阶的高度 可以改写成连续差形式(分数拆分) 伸缩和
或者说发现物理问题的 数学模型!
光滑和光滑的崩解
毕加索:“艺术是让我们认识真理的谎言”
重新定义我脑子里的光滑的概念:如果一条曲线在任何一点处被充分放大后,它越来越直,那么它是光滑的!(充分是要有个度的,就像煮熟和烧焦中间的那个度~)
连续-光滑——可导——微积分 如果我们设法把测量的分辨率推升得过高,在时空中极其细微地观察任何现象,就会看到光滑度的崩解。
和所有科学领域一样,在建立数学模型时,我们总要对强调什么和忽略什么做出选择。抽象的艺术在于 知道什么是必不可少的,什么是细枝末节的;知道什么是信号,什么是噪声;知道什么是趋势,什么是波动。
就像前面的关于无穷小的讨论中,对微分方程的处理,正是通过忽略高阶无穷小的部分才得到了函数y=x^3的导数表达式dy/dx=3x^2
某个奥运冠军的跑步时 低频拍照记录得到的位置-时间图、及其推算出的速度-时间图、高频拍照记录推算出的速度-时间图
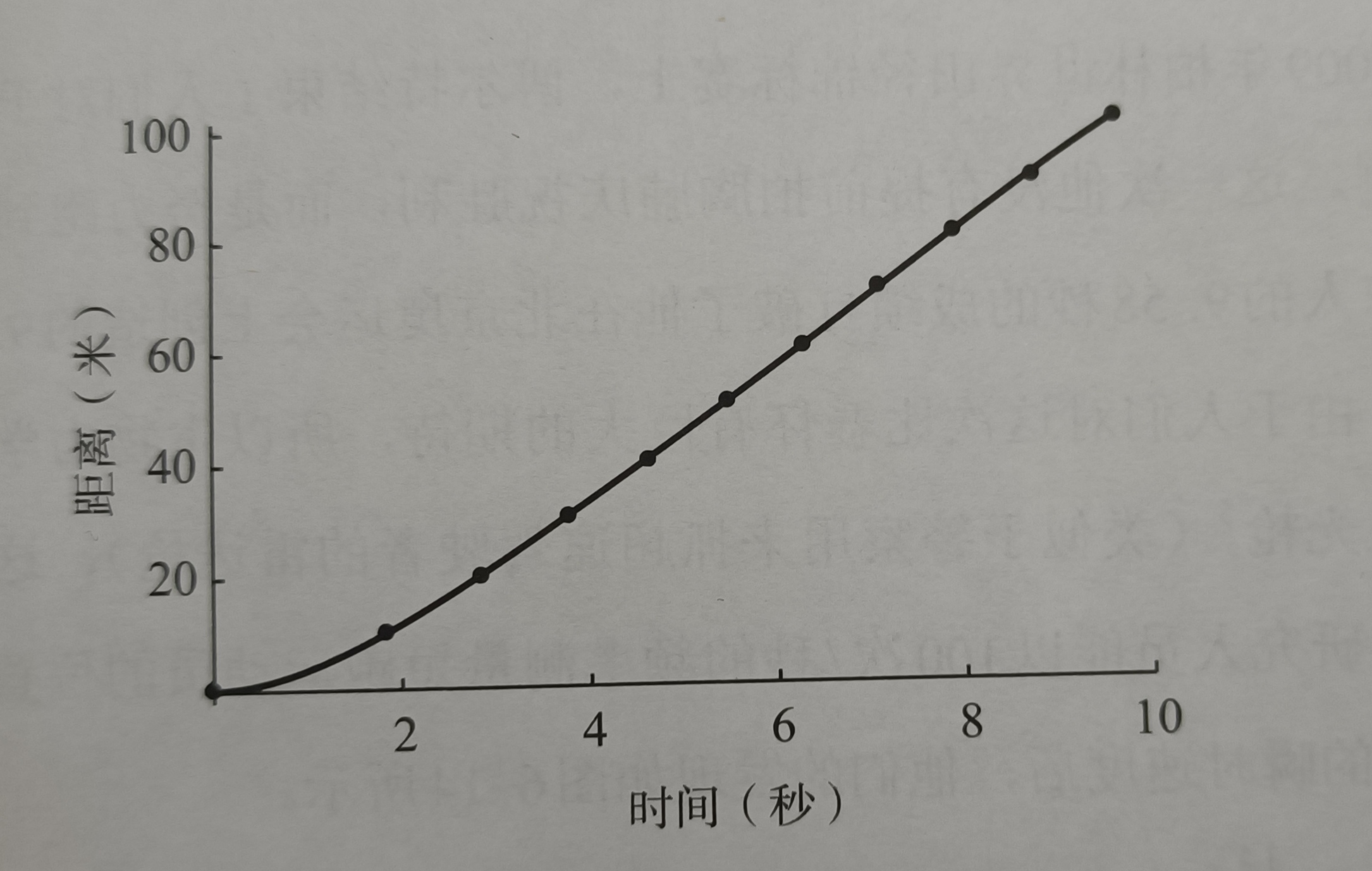 |
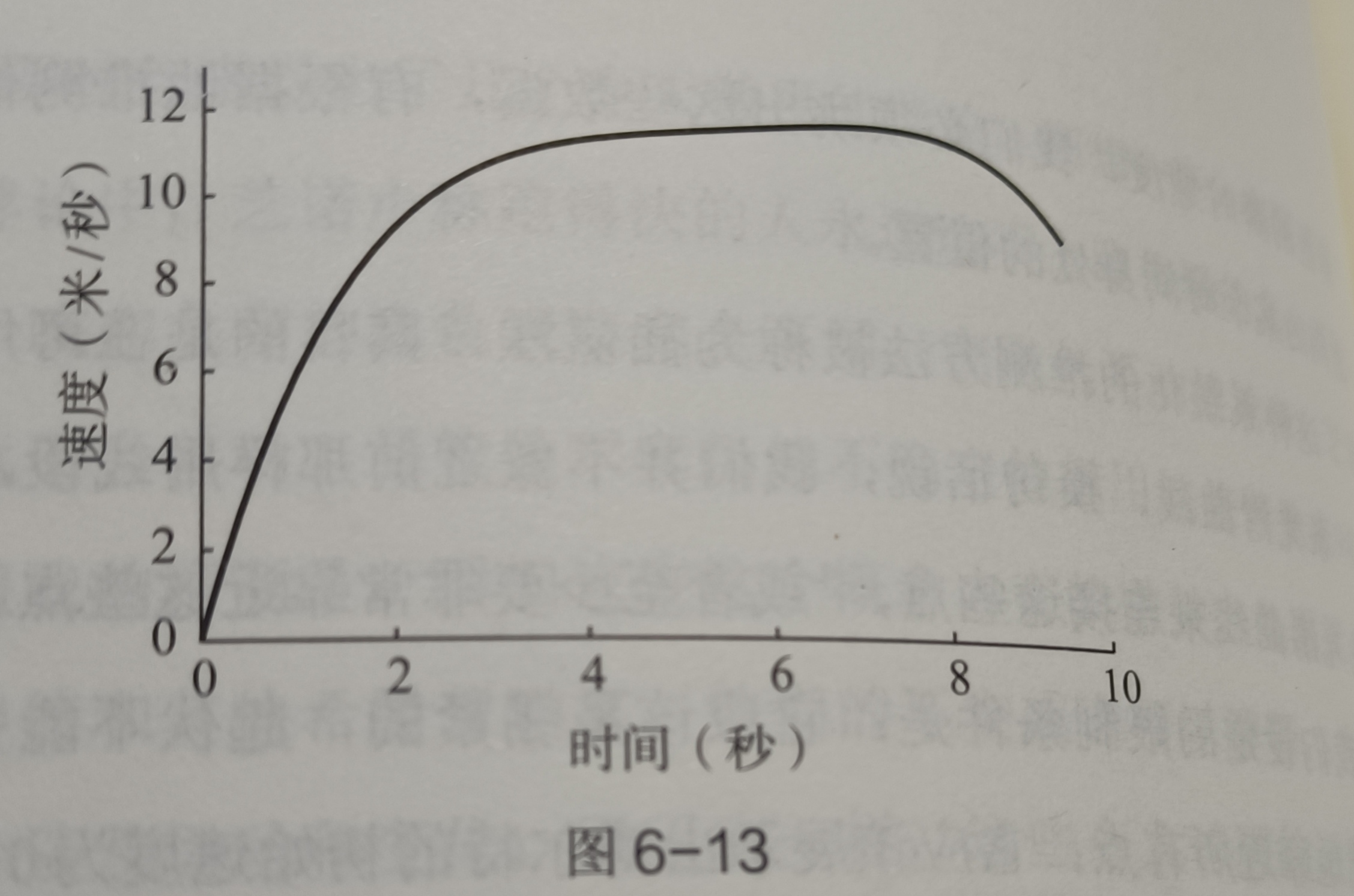 |
 |
|---|---|---|
| 低频 位置-时间 | 低频 速度-时间 | 高频 速度-时间 |
再如对任何研究对象,如果分辨率高到原子级,那么一切都不连续或光滑了。
科学的审美/直觉
简洁美
背后的艺术性,通过提出一个美丽的问题,伽利略从大自然那里“哄骗”出一个美丽的答案。他就像一位抽象表现主义画家。
纵观这些科学家发现的公式科学、公理定律,无不透露着简洁的美,似乎越是简洁的公式定理越是强大地令人震惊,比如爱因斯坦的质能方程式
尽可能忽略掉噪音的影响将变量数最小化,获得了简洁的理论
简洁和最小化是很棒的审美
连续体和离散体以及 微分方程
比如我们来看一碗汤
- 离散的角度(实际),一碗汤是一堆离散的分子,它们都在杂乱无章的跳跃。每个分子为对象,自变量是时间t
- 对象太多了
- 每个对象的运动都太过复杂!
- 单自变量,每个对象对应一个常微分方程
- 连续的角度(近似),看成是一个连续体,连续体的各个位置(x,y,z)和时间t都是自变量!
- 多自变量
- 一个偏微分方程!
连续体假设 这在流体力学中很常见!!!当时不太能理解那些偏微分方程!
弹性、声学、热流、流体流动和气体动力学的定理公式很多都是偏微分方程。
现代科学中的微积分应用主要体现在偏微分方程的建立、求解和解释!
牛顿微积分与独立宣言
数学与人文、哲学的瓜葛
牛顿的经验演绎法,以事实为基础,以微积分 为动力,扫除了早期哲学家的先验形而上学方法。
牛顿的思想还在从决定论和自由到自然律和人权等所有启蒙观念上留下了印记
独立宣言
- 效仿欧几里得在《几何原本》和牛顿在《原理》中的做法,也从公理(与主题相关不证自明的真理)着手,然后凭借逻辑的力量,从这些公理中推导出一一系列不可回避的命题。其中最重要的一个就是殖民地有权脱离英国的统治
数学在人文哲学上应用,体现在数学思维的运用。
隐藏在小学题里的微积分
无限循环小数0.333…=1/3,
追击问题,兔子追乌龟,兔子10米每秒,乌龟1米每秒,起点乌龟领先10米
微积分的思想:
1秒后兔子追平落后的10米,此时乌龟又领先1米
0.1秒后兔子追平落后的1米,此时乌龟又领先0.1米
0.01秒后兔子追平落后的0.1米,此时乌龟又领先0.01米
...
相当于无穷级数1+0.1+0.01+…=1.11…=10/9
当然还有另外的求解方法。比如设兔子追上乌龟用时为t秒,10t=10+t,就可以解得t=10/9。
最早接触到无穷还是小时候
在操场上,无穷曾以嘲弄和抬杠的方式出现:
你是个混蛋!
是啊,好吧。你是两倍的混蛋!
你是无穷倍的混蛋!
你是无穷加1倍的混蛋!
那和无穷倍是一样的,你这个笨蛋!
无穷+无穷还是无穷,但无穷的无穷倍就不一样了,就像一个具体数字(常量)表示的级数和,和一个用x(变量)表示的级数和后者是牛顿创造的通用级数法,他代表的是无穷个无穷~~显然比任意单个无穷强大~
万物皆数?
万物皆波
用傅里叶的方法可以分析各种波现象,热核爆炸的冲击波,通信的无线电波,在肠内促使营养物质吸收并推动废物朝着正确方向移动的消化波,大脑中与癫痫和帕金森震颤相关的病理性电波,公路上的交通拥挤波。脑电波、心率波
科学、数学与音乐之间的关联蛮奇妙~ 正弦波+正弦波可以得到三角波,进而多个正弦波叠加可以得到任意一种波? 纯音+所有泛音就形成了三角波。这是一个正弦函数表示的无穷级数和。三角波公式 (纯音如公式中的sin(x),泛音如sin(3x)、sin(5x)) 任何乐器的时声音都可以用无穷多个音叉合成,我们要做的只是在适当的时间用适当的力度敲击音叉。电子音乐合成的原理~~~
正弦波的音干净而宽广如长笛,方波的音尖利而刺耳如警报,三角波的音喧闹嘈杂。
正在他们的眼里或许 真是万物皆数吧 好奇妙
DNA的缠绕数
- 在你大约10万亿个细胞中,每个都有约2米长的DNA,如果它们收尾相连,那么足够在地日间往返几十次。
- 一个典型的细胞核的直径约为5微米,它是细胞内DNA长度的40万分之一,这个压缩系数相当于把20英里长的绳子塞到一个网球里。
DNA包含了一个人成长发育所需的全部遗传信息,这么长也是理所应当的吧~
DNA双螺旋我知道,但不知中间还有一根线轴,以及它们有序的打包方式~
- DNA打包的形象比喻。你拉紧一条橡皮筋,用手指夹住它的一端,并从另一端扭转它。刚开始橡皮筋每次转动都会产生一个扭结,当积累的扭转超过临界值时,橡皮筋不再保持绷直状态,而会突然弯曲并盘绕在自己身上,仿佛在痛苦地扭动。最终橡皮筋聚成一团。实现了压缩。DNA也是这样做的。
- 扭曲和缠绕之间的转换,就好比一团卷好的水管,你去抽出来这种缠绕会转变扭曲,也就是你拿到的水管总是扭曲了很多个扭结的原因。或者我觉得可以拿风筝线来描述会更有体会,尤其质量不太好的风筝线感受最深,从线圈出来后就是有很多个扭结的,让强迫症心烦!
GPS定位精度
你知道吗,当一个物体穿过引力场时,时间的流逝可能会加快或者减慢。GPS卫星就需要考虑这一点,哪里的引力场较弱,会使时空曲率扭曲,并导致钟表比在地面上走时快,每天都会比地面上的时钟快45微妙,这听起来似乎不太多,但别忘了GPS需要纳秒级的准确度才能正常运转,而45微秒是45000纳秒,如果没有广义相对论的修正,GPS的误差将以每天10千米的速度不断累计,整个导航系统在几分钟之内就会失去导航价值。
神秘
拉普拉斯妖
拉普拉斯设想的一种全知全能的智慧生物,它可以追踪宇宙中所有原子的所有位置,还有作用于他们的所有力。“如果这个智慧生物也能对这些数据进行分析,那就没有什么是不确定的了,未来也会像过去一样呈现在它眼前”
超奇妙的设想,堪称一部科幻巨作。然而三个陀螺让它终结了~ 也有说是倒在了热力学和量子力学脚下的。
混沌 新认识
开始方式的小小改变,也会产生大不相同的结果。
初期或许还可以预测,但是后期就完全失控。这个时间界限就是可预测性时界,整个太阳系的大概是400万年。
作为漂浮在一个中量级星系中的一颗微不足道的行星上的一个无足轻重的物种,智人是如何成功预测出,在距离地球10亿光年之遥的浩瀚宇宙中的两个黑洞相撞后,时空会发生怎样的震颤呢?我们早在引力波到达地球之前,就知道他的声音应该是什么样子了。
知道的越广,越发现自己的渺小和无知。
